Explanations
Most users will log into OTTER after they have spent several hours engaging in lessons and after-school activities. They will be physically and mentally exhausted, and will try to go through questions as quickly as possible, even if this causes them to make silly mistakes. Unfortunately, most pupils lack the patience and the stamina to read and assimilate verbose explanations, which often information that is not strictly relevant.
It follows that all introductory and supplementary explanations need to be as incisive as possible. They should not overwhelm the user with excessive details or references to previous question templates.
If an OTTER user wants more information after reading an explanation, s/he can always obtain further insights by either googling keywords or checking reference books.
Fortunately, many question templates do not require either an introductory or a supplementary explanation. The examples of them are explained below. You can read about Otter questions in answers in more detail in Guidelines for Math writers.
Introductory Explanations
Very few maths question templates provide introductory explanations.
Introductory explanations are included in maths question templates only when it is unlikely that the subject has been taught comprehensively in British schools. Introductory explanations in maths question templates tend to be longer than those in English question templates, as can be seen in Examples 5 and 6 below.
Again, as for English question templates, the general rule is: If a question template does not provide an introductory explanation, do not include one in your new question. If an question template does provide an introductory explanation, just retain the identical wording in your new question.
Below are two examples of maths question templates which provide introductory explanations.
Example 1 (The introductory explanation is in two parts: a statement of a mathematical rule and then a worked example before the question.)
When two events are mutually exclusive, we can calculate the probability of either of the events happening by adding together their individual probabilities. To do this, we use the Addition Rule (OR Rule):
|
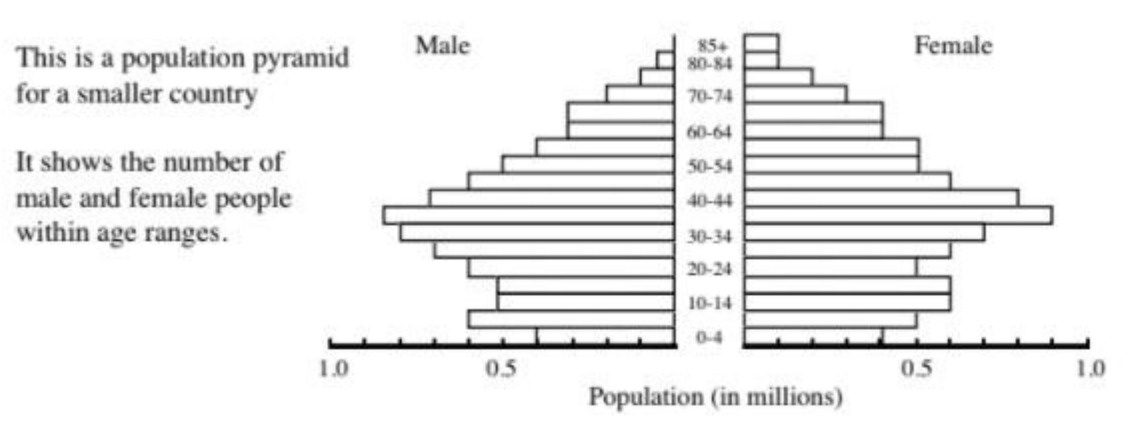
Example 2 (The introductory explanation is in two parts: an explanation of what the diagram shows and a worked example before the question.)
Example: In the 0 – 4 age range, there are 0.4 million females and 0.4 million males. Question: What are the populations of females and males in the 40 – 44 age range? |
Supplementary Explanations of Correct Answers
In maths subtopics, every supplementary explanation should focus narrowly on the question at hand and should avoid references and/or comparisons to similar problems.
Most importantly, every supplementary explanation must be presented as a ‘worked example’.
What is a ‘worked example’? A worked example is a line-by-line solution that is easy to read in steps. It is essentially what a teacher would write on the blackboard in a classroom when she is showing her students how to solve a problem.
A worked example may not have any text at all or it may contain up to three bullet points of text which highlight general rules or principles of mathematics.
Of course, some worked examples contain little if no ‘working’. For example, the sum ‘2 + 2 = 4’ cannot be elaborated much further, except perhaps by representing the sum as some type of diagram, such as // +// = ////.
As a general rule, supplementary explanations should be kept as short as possible and may include a diagram, if a diagram is the best shortcut to understanding.
Six examples of supplementary explanations in maths question templates are shown below in Examples 3 – 8.
Example 3 Estimation Difficulty Level 4
Tom sells 1506 books that each cost $6.95. Estimate the amount of money that Tom made from the sale of his books. Multiple-choice options are presented and the correct option is identified. ------------------------------------------------------------------------------------------- Supplementary explanation: Round both numbers to the nearest whole number 1506 ---🡪 1500 $6.95---🡪 $7 Estimate of money made = 1500 x $7 = $10,500 |
Example 4 Range, Difficulty Level 4 Question Template
The concept of “spread” (variation or dispersion) is very important in statistics. So far, the only way we have encountered measuring it has been to use the range, but that’s a very crude measure. For a more accurate and reliable measure of range we use the interquartile range. Example: Here is the number of the detentions given this week by 15 teachers in ascending order. 12, 13, 21, 28, 29, 31, 31, 32, 33, 34, 38, 41, 42, 49, 73 where 28 is 1st quartile, 32 is 2nd quartile (or median), and 41 is 3d quartile. The one in the middle is the median. The other 2 numbers highlighted split the numbers into quarters, and so are called the first and third quartiles, Q1 and Q3 (the median is Q2). The difference between these values is a valid measure of dispersion of the data about the average figure. Therefore, the interquartile range (IQR) is Q3 - Q1, in the example above 41 - 28 = 13. The interquartile range isn’t affected by extreme values. It only uses the middle half of the data. What is the median and interquartile range of the set of data below? 47, 42, 60, 49, 37, 40, 17 Multiple-choice options are presented and the correct option is identified. --------------------------------------------------------------------------------------------------- Supplementary explanation: Place the numbers in ascending order: 17, 37, 40, 42, 47, 49, 60 Median = the middle number = 42. Q1 = number at first quarter point = 37 Q3 = number at third quarter point = 49 The interquartile range = Q3 – Q1 = 49 – 37 = 12 |
Example 5 Working with Brackets, Difficulty Level 5
Multiply out and simply the algebraic expression below. 2 ( 3a + 4 ) + 3 (a + 2 ) Multiple- choice options are presented and the correct option is identified. -------------------------------------------------------------------------------------------------
|
Example 6 Compass Directions and Bearings Difficulty Level 3 Question Template
What fraction of a turn is there from N to SW on a compass? Multiple-choice options are presented and the correct option is identified.
--------------------------------------------------------------------------------- Supplementary explanation: Going clockwise from North to South = 180 degrees = 180/360 = 1/2 Continuing clockwise from South to Southwest = 45 degrees = 45/360 = 1/8 Therefore, going clockwise from North to Southwest = 1/2 + 1/8 = 4/8 + 1/8 = 5/8 |
Example 7 Percentages-Decimals-Fractions Conversions Difficulty Level 2 Question
Template
Change 12% into a fraction and a decimal. Multiple-choice options are presented and the correct option is identified. --------------------------------------------------------------------------------------------- Supplementary explanation: Fraction: 12% = 12/100 = 6/50 = 3/25 Decimal: Divide 12 by 100 = 0.12 |
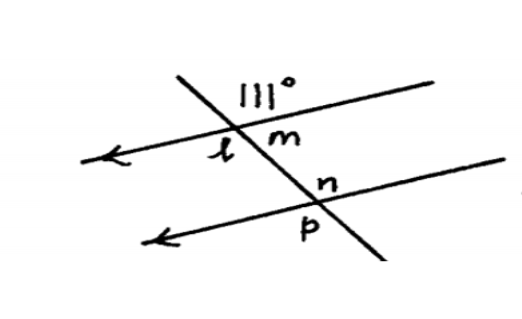
Example 8 Lines and Angles Difficulty Level 2 Question Template
|
Find the sizes of angles m, n, l and p.
Multiple-choice options are presented and the correct option is identified. ---------------------------------------------------------------------------------------- Supplementary explanation (more than one solution possible): Vertically opposite angles are equal so l = 111 Angles on a straight line add up to 180 so 111 + m = 180 and m = 180 – 111 = 69 Interior angles add up to 180 so m + n = 180 so n = 180 – 69 = 111 As p and n are vertically opposite, p = n = 111 |
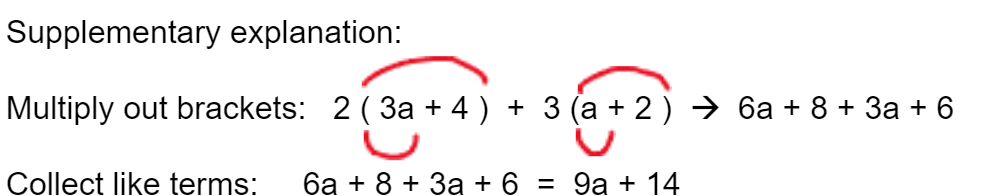
No Comments